介绍

也是一篇在CTR预估中堆Deep层数的轮子文，先来了解一下：

1. DeepFM：使用FM的特征组合能力灌给DNN进行joint-train
2. Deep&Cross：根据首层和次层的依赖可以解决多阶特征组合的问题

不过xDeepFM所提出的点是结合RNN和CNN的特性完成多阶特征的抽取，并且最终和和DNN以及Linear整合到一起完成显性特征的使用。

CIN

据说有RNN和CNN结合的xDeepFM中最重要的核心元素是CIN（Compressed Interaction Network）
一个图来解释CIN: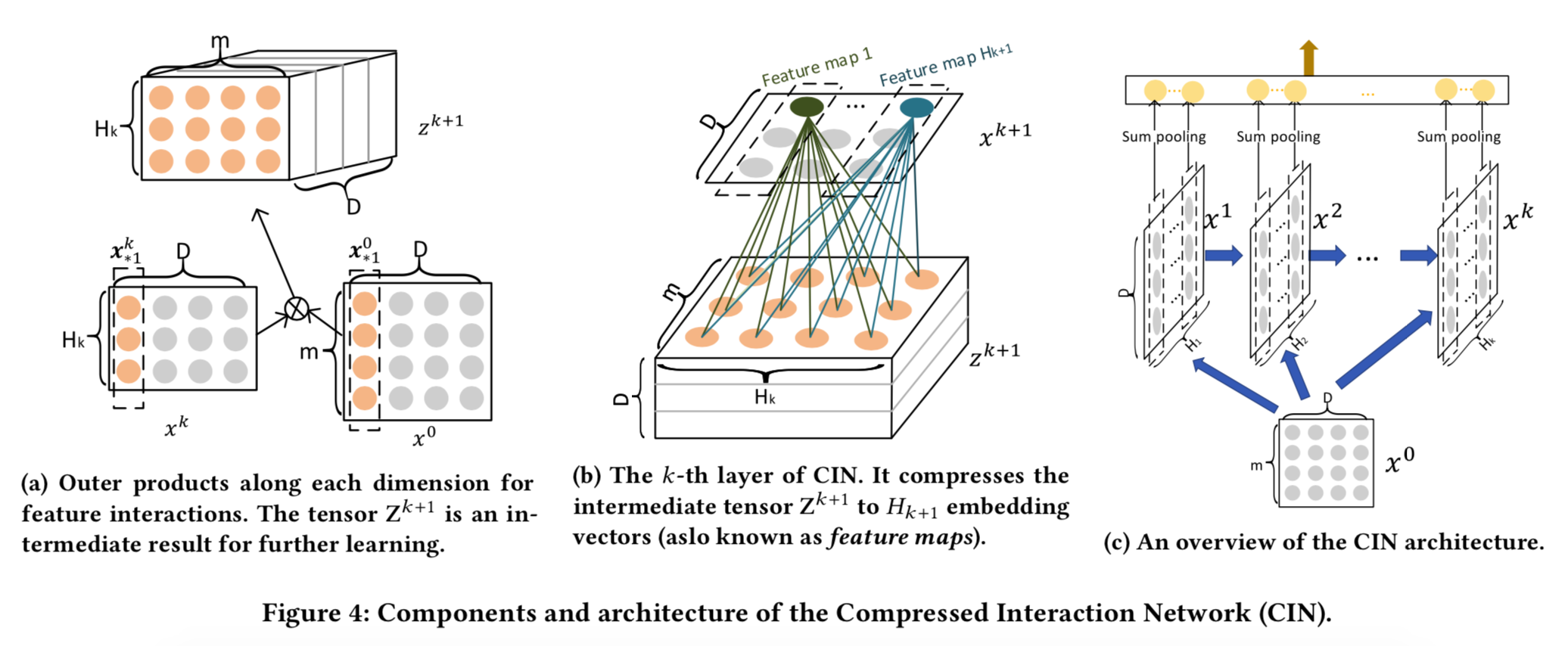

这里：

1. 我们输入的是一个m个特征的D维Embedding数据，简称$X^0 \in R^{m \times D}$,这个作为第一层
2. 然后CIN有设计一种计算下一层的式子：$$X_{h,*}^k = \sum_{i=1}^{H_{k-1}} \sum_{j=1}^m W_{i,j}^{k,h}(X_{i,*}^{k-1} \circ X_{j,*}^0)$$
   1. 这里的$\circ$符号表示点击，$(a_1,a_2,a_3) \circ (b_1,b_2,b_3) = (a_1b_1,a_2b_2,a_3b_3)$
   2. 整个式子可以分解为两份，类RNN和CNN
   3. 在计算$X^k$时是依赖$X^{k-1}$的，所以类似RNN那种是依赖上一个状态，同时里面还引入了$X^0$，其实是参考了Deep&Cross的做法，这一步形象的画出来就是上图(a)
   4. 他们一步完成之后会产生一个中间状态$z^{k+1}$，是一个三维的张量，其实基于$W$矩阵的投射可以重新转为一个二维的$X^{k+1}$，其实是类似一个CNN的卷积过程，就是图中$b$
   5. 这些深层级的$X$计算完毕之后，使用一个sum pooling将各个feature map进行聚合$$p_i^k = \sum_{j=1}^D X_{i,j}^k$$
   6. 将所有的聚合层concat之后得到$p^+ = [p^1,p^2…p^T]$
   7. 再通过激活函数得到最终的结果$$y=\frac{1}{1+exp(p^+W)}$$

这儿CIN各种复杂度：

1. 他的参数复杂度是:$\sum_{k=1}^T H_k \times (1+H_{k-1} \times m)$
   • $T$表示CIN的总层数
   • 每一层的W参数是$H_k \times H_{k−1} \times m$
   • 顶部线性成的参数量是$H_k$
2. 他的计算复杂度是:$O(mH^2DT)$
   • 他单层的$Z^{k+1}$的计算复杂度是$O(mHD)$
   • 并且额外的我们还需要将feature maps汇聚到$H$个隐藏节点

xDeepFM

最终的xDeepFM的大结构是参考了Wide&Deep的方式: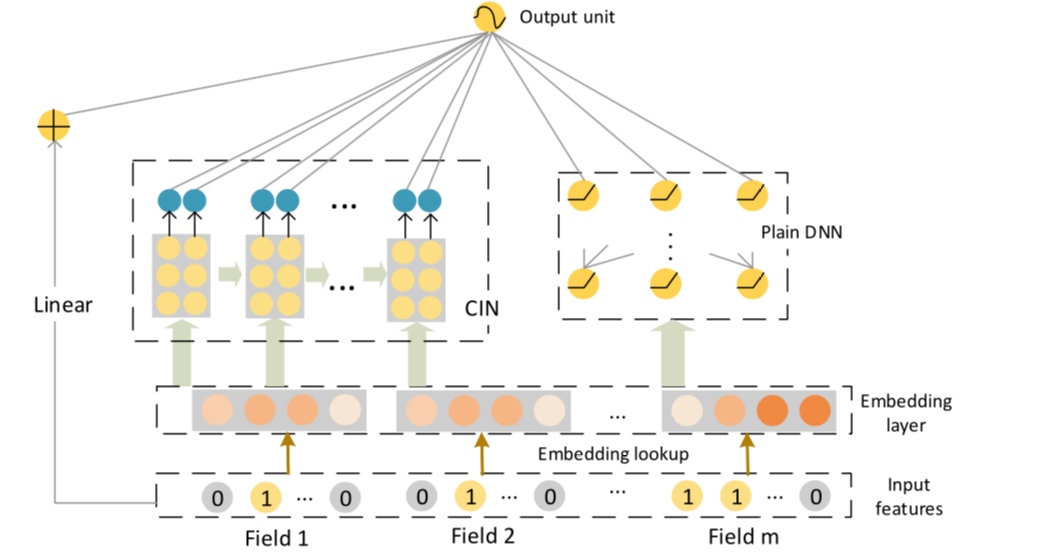

1. 最左侧是一个线性模型（其实这儿是一个稀疏层）
2. 中间是上面刚刚描述的CIN模型
3. 最右侧其实就是一个传统的DNN模型了
4. 最终将所有的隐藏层的值合并进行了计算：$$y=\sigma(W_{\text{linear}}^T a + W_{\text{dnn}}^T x_{\text{dnn}} + W_{\text{cin}}^Tp^+ + b)$$

他和DeepFM的关系：如果将CIN这一层里面的层数改为1，他其实就是一个FM

实验结果

里面描述的实验结果中，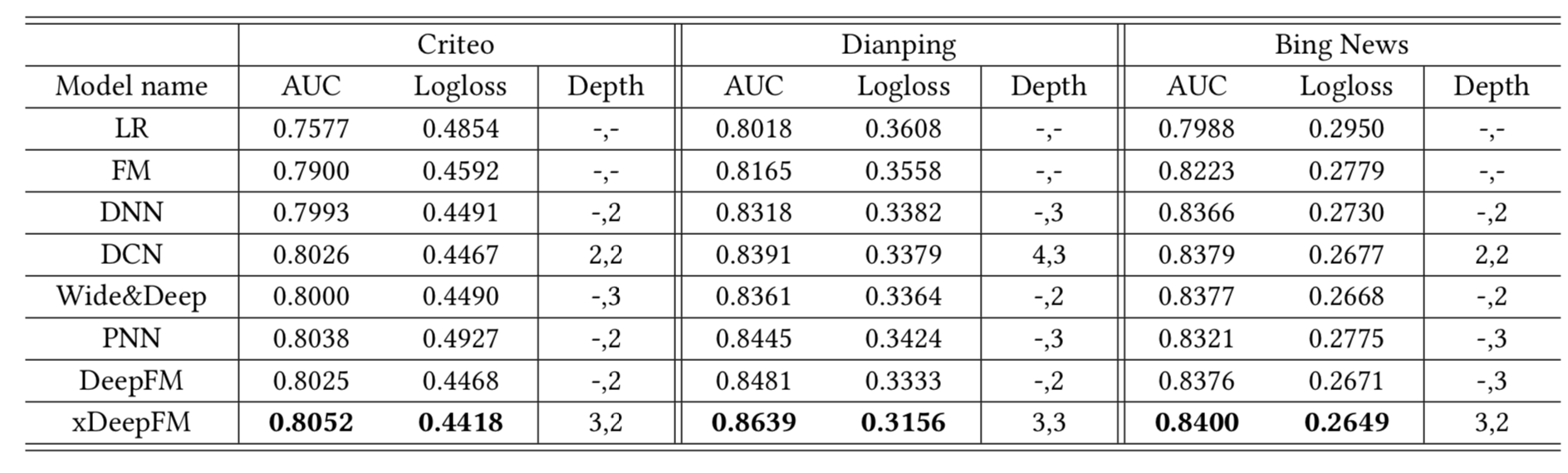

看起来xDeepFM还是有一些提升的，不过主要提升是在DianPing数据集上，另外两个数据集提升的还是很微弱，在这种复杂度下，计算性能和带来的效果回报的受益就比较低了。

总结

1. 感觉xDeepFM主要引入了Deep&Cross里面的Cross机制，就是在做堆叠
2. 另外其实看到堆叠和交叉还是能带来一定效果的，但是受益越来越不明显了，如果运行性能和算法性能的性价比，FM无疑是最高，但是Deep模型可以说故事（chui）啊
3. 作者开放了源码，赞一个

文献

1. Lian, Jianxun, et al. “xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems.” arXiv preprint arXiv:1803.05170 (2018).